

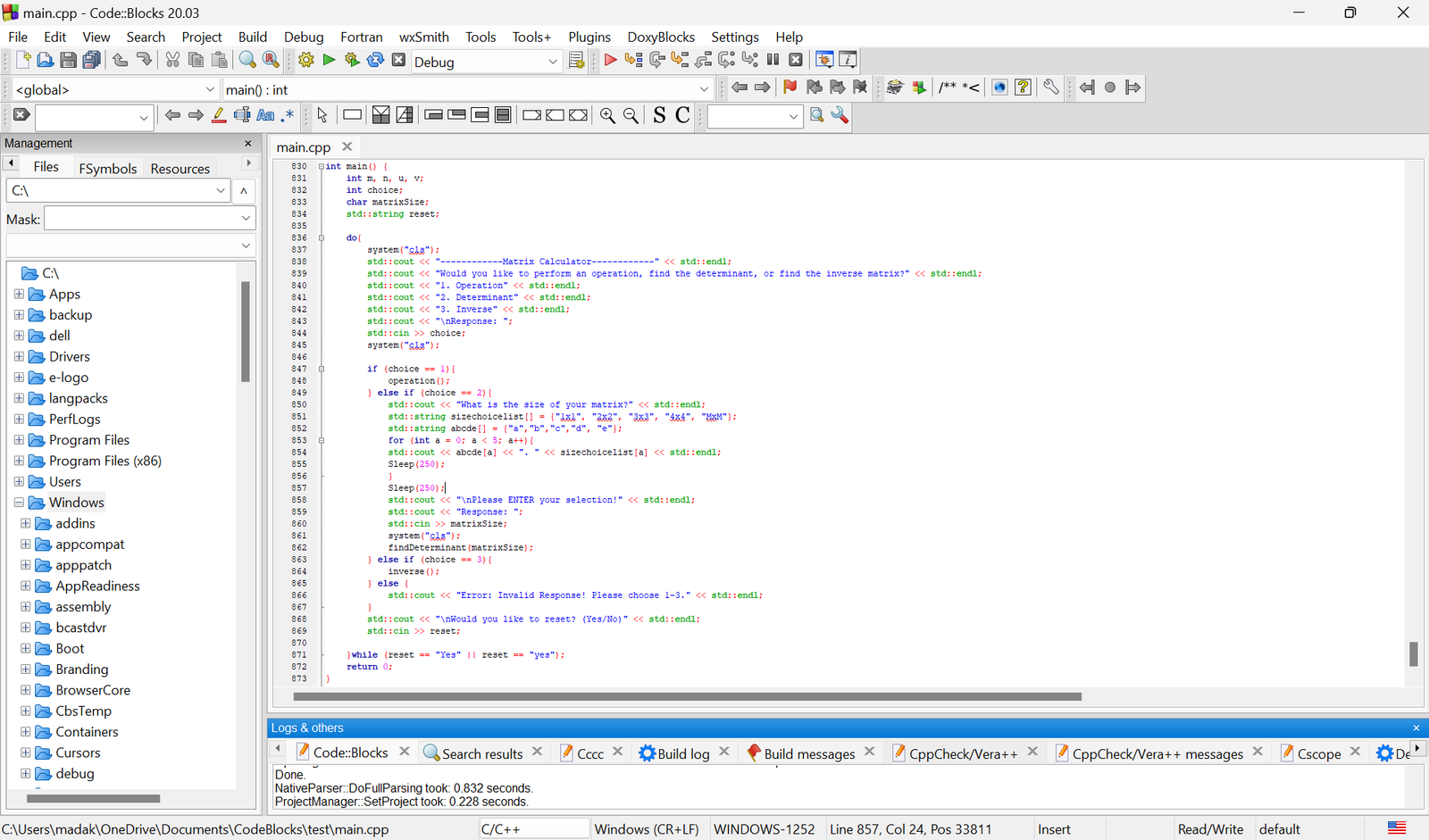
This project aims to develop a versatile tool in C++ for handling unpleasant calculations involving matrices, inspired by a passion for mathematics and a desire to prepare for an upcoming computational linear algebra course. Initially conceived as a program to explore physics concepts such as wave-particle duality theory, the project shifted focus due to time constraints. The decision to create a matrix calculator arose from the desire to gain early exposure to linear algebra, a field with wide-ranging applications in fields like circuit modeling, graphics rendering, robotics, and differential equations. While the original physics-related idea remains a passion project for the future, the current focus is on building a solid foundation in linear algebra through practical programming.
This C++ project encompasses a comprehensive matrix calculator, featuring the basics from operations like addition, subtraction, and scalar vs. matrix multiplication to progessive calculations. The implementation involves a progression of complexity, with functions becoming more intricate and recursive as operations expand. The project navigates challenges such as memory management, readability, and complex calculations, opting for vectors over raw pointers for scalability and readability. Particularly, the determinant and inverse functionalities employ recursive functions to handle matrix sizes dynamically, with the inverse feature relying on the adjugate method for computation. Through meticulous coding and problem-solving, the project delivers a robust tool for matrix operations while addressing complexities inherent in linear algebra computations.
The program also utilizes dynamic memory allocation to generate matrices based on user-defined dimensions, enabling flexibility and scalability, allowing users to work with matrices of various sizes, from small to large dimensions. Without memory allocation to release memory dynamically after each computation, the excessive amount of memory required to perform such task on a large scale would be an inefficient use of the program’s resource, thus this would lead to inefficiency and limitations on the size and performance of the program.
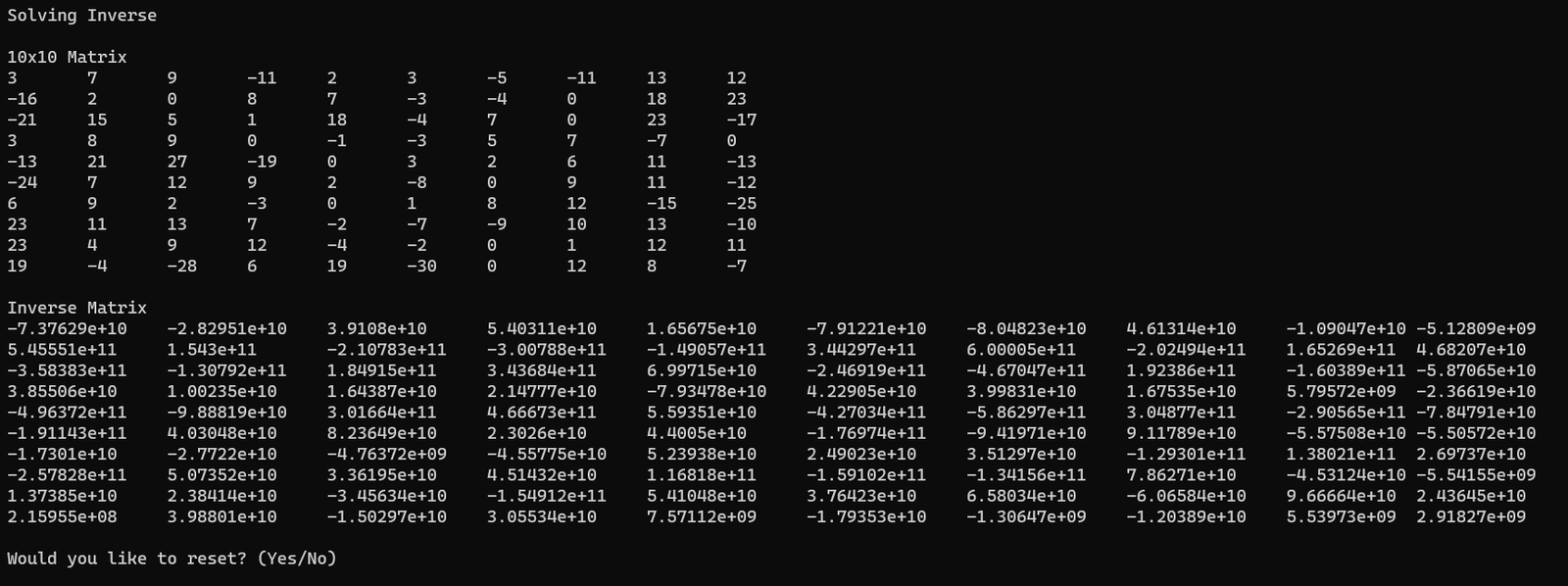
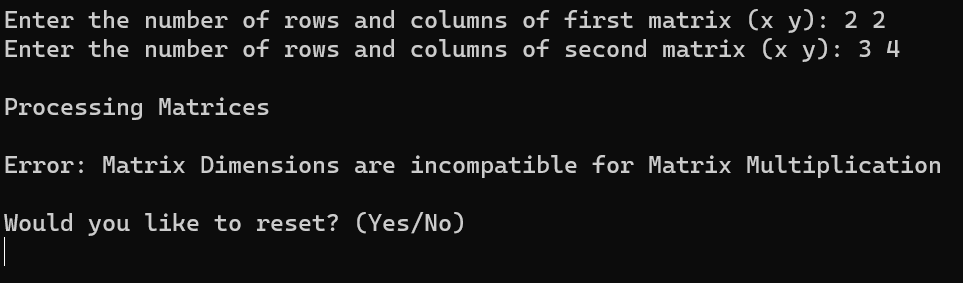
The program employs error management to validate user inputs, focusing on matrix size compatibility and invertibility. Addition and subtraction require matching dimensions, while multiplication demands alignment between matrix columns and rows. Determinant computation mandates perfect square dimensions, while inversion necessitates a square matrix. However, rare cases, especially with larger matrices, may lead to undefined inverses if the determinant or any submatrix's determinant is zero during the adjugate method. In working with inverses of MxM matrices, I discovered that vectors offer efficiency advantages over raw pointers due to their self-managing nature, eliminating the need for explicit memory allocation and facilitating manipulation through recursive loops after function defining.


• Finding patterns in the adjugate method of solving large size matrices
• Processing excessive number of nested loops and variables
• Conversion issues between raw pointers and vectors
• Ensuring recursive functions do not tamper with outside variables
• Writing more efficient methods of code in solving the same problem
• Learning properties of matrices using online linear algebra resources
• Ensuring consistency of outputs regardless of significant figures
• How to utilize vectors to simplify a task regarding multiple arrays
• How to utilize vectors to simplify a task regarding multiple arrays
• New and unfamiliar C++ libraries and their built-in functions
• Memory allocation is unnecessary when vectors are destructed
• Practice in function arguments, debugging, and testing C++ code
• How to create recursive functions to solve mathematical loops
• A handful of non-included properties of matrices