Overview
I built this console tool to get comfortable with linear algebra before taking a computational linear algebra course. The original idea started as a physics-focused simulator, but I pivoted into a matrix engine because it’s foundational: circuits, robotics, graphics, state estimation, and differential equations all depend on reliable matrix operations.
Goal
Make a reusable CLI tool that computes core matrix operations for arbitrary sizes with clean output and strong input checks.
Key takeaway
Writing the math from scratch forces you to understand what libraries normally hide: constraints, edge cases, and numerical pitfalls.
Features
The console supports basic operations (addition, subtraction, scalar/matrix multiplication) and more advanced routines like determinants and inverses. As the feature set grew, the code naturally pushed toward structured implementations: reusable helper functions, consistent formatting, and recursion for operations that scale with matrix size.
Operations supported
• Add / subtract (same dimensions)
• Multiply (dimension-aligned)
• Determinant (square matrices)
• Inverse (square + non-singular)
Implementation highlights
• `std::vector` for safety + readability
• Recursive minor expansion for determinants
• Adjugate-based inverse (with validity checks)
• Defensive input handling for constraints
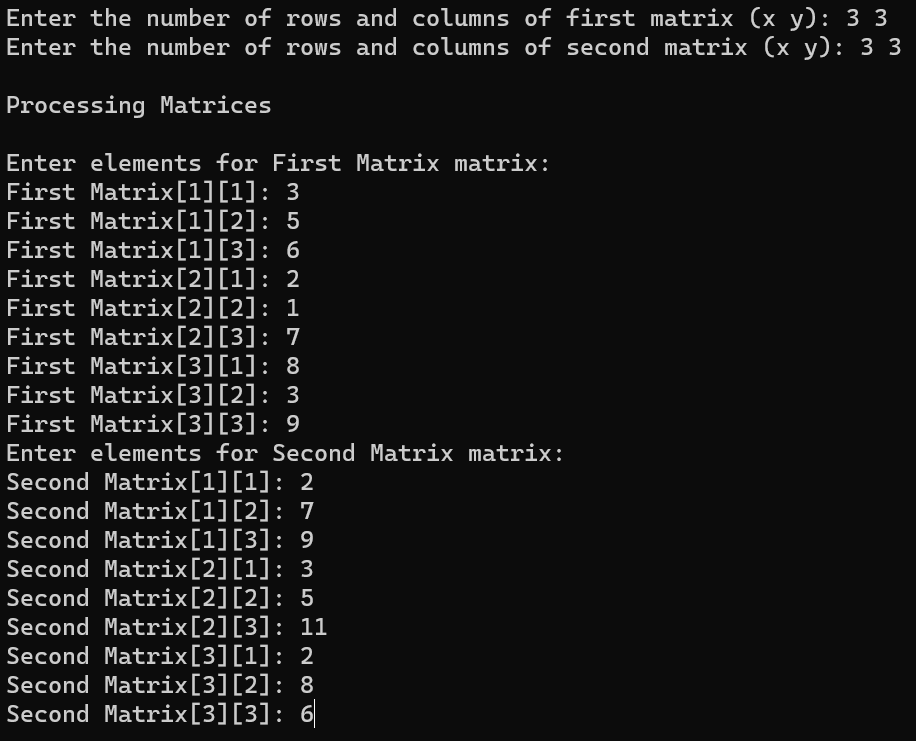
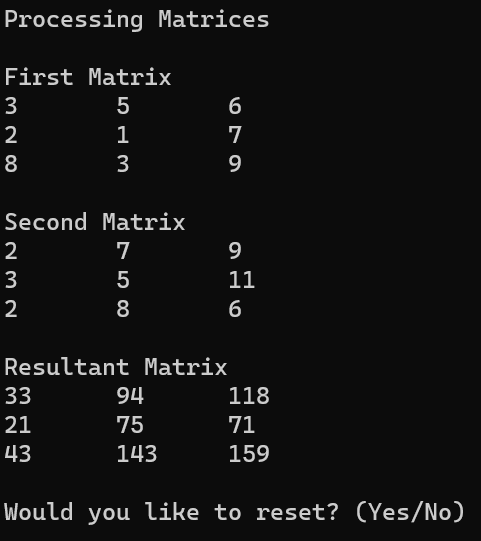


Memory & Scalability
Matrices are created at runtime using user-defined dimensions, which makes the calculator flexible for both quick 2×2 checks and larger test cases. I initially considered raw pointers, but moved to vectors to reduce memory bugs and simplify ownership. With vectors, allocation and cleanup happen safely through scope, which made iterative testing much faster.
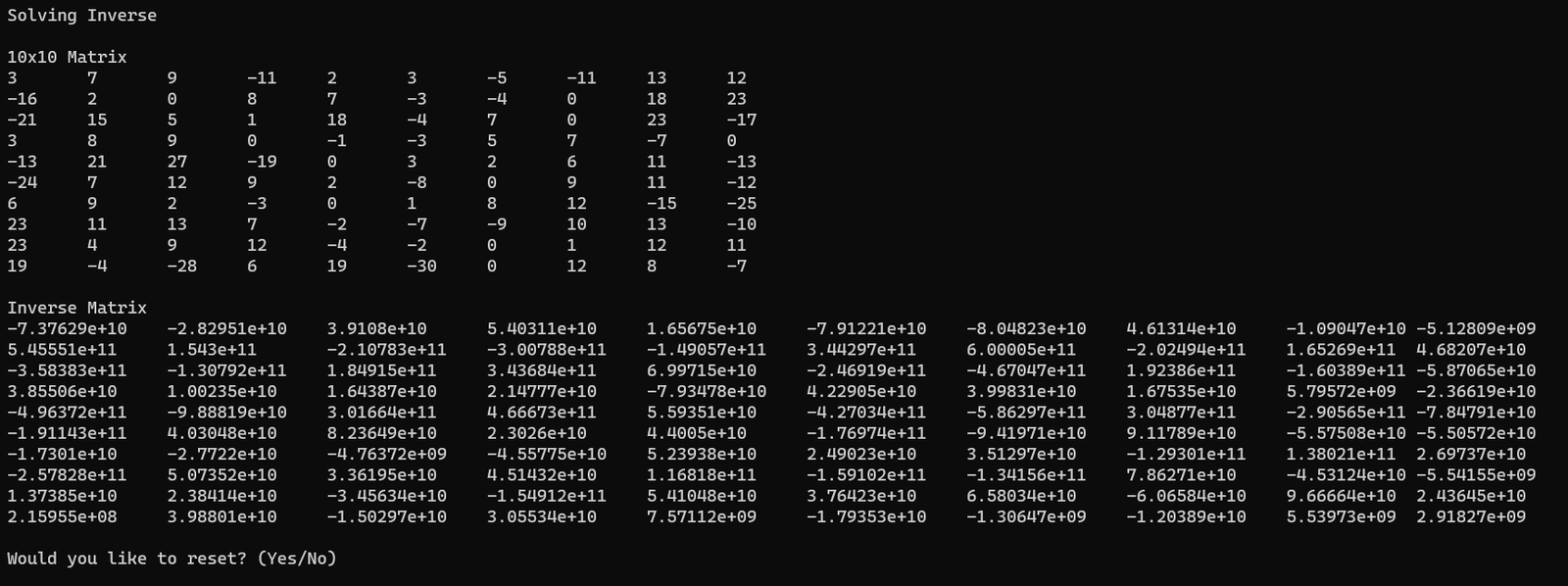
Why vectors
Automatic lifetime management, bounds-friendly iteration, and easier recursion without pointer bookkeeping.
Scalability note
The adjugate/inverse path becomes expensive for large matrices, which motivates future upgrades (LU/Gauss-Jordan) if this evolves into a faster tool.
Validations & Edge Cases
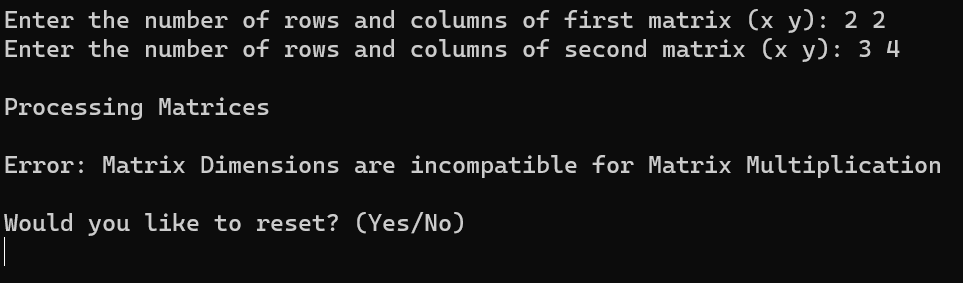
A huge part of making the calculator “feel reliable” was error handling: rejecting incompatible dimensions early and preventing undefined operations. Inverse computation is only valid for square, non-singular matrices. For larger matrices, singularity can appear through determinant = 0 (or intermediate minors evaluating to zero during expansion), so the program detects and communicates those cases instead of producing garbage output.
Compatibility rules
• Add/subtract: same rows + columns
• Multiply: A.cols == B.rows
• Determinant: square only
• Inverse: square + det ≠ 0
Practical improvements
Clear prompts + consistent formatting made debugging easier and reduced user input mistakes, especially when working with larger dimensions.


Results
The final console tool reliably executes common matrix workflows and enforces the mathematical constraints that matter. The biggest win wasn’t just “it works”, it was learning how to design code that stays readable as complexity grows (especially with recursion and nested loops).
What worked well
• Strong input validation prevents bad states
• Vector-based structure kept memory sane
• Determinant/inverse generalized to NxN
Next upgrade
Replace adjugate-based inverse with Gauss-Jordan or LU decomposition for speed and better numerical stability on larger matrices.
Reflection
Challenges
• Managing deep nesting and keeping logic readable
• Designing recursion that doesn’t leak state across calls
• Handling singular matrices and edge cases cleanly
• Consistent numeric formatting for outputs
What I learned
• Safer dynamic structures with `std::vector`
• Recursive decomposition for determinant expansion
• Cornercase handling + validation logic
• How linear algebra constraints translate into code

 by Justin Yu
by Justin Yu