Overview
The goal of this project was to classify cat vs dog images using multiple supervised learning methods and evaluate their performance on a shared dataset. I implemented and compared: Closest Average (CA), Linear Discriminant Analysis (LDA), Quadratic Discriminant Analysis (QDA), and Nearest Neighbor (NN). I also explored Principal Component Analysis (PCA) to reduce dimensionality and studied how the number of retained components affects error rates.
What I built
• A consistent pipeline to train/test multiple classifiers on the same splits
• PCA feature compression + analysis vs k dimensions
• Error-rate comparisons to understand bias/variance trade-offs
Why it matters
Classical methods still matter in real systems: they’re interpretable, efficient, and great for building intuition about data geometry and representation.
Dataset
The dataset consists of labeled images (cat or dog). Images are vectorized into feature vectors for classical ML methods. PCA is applied using training statistics and then reused on the test set to avoid leakage.


Supervised Learning
I implemented multiple supervised classifiers using the same train/test splits to compare performance fairly. Results were evaluated using training vs testing error to measure generalization and sensitivity to feature dimension.
Classification
Supervised learning is implemented through classification techniques that rely on labeled data. Closest Average (CA) assigns labels based on distance to class mean vectors. Linear Discriminant Analysis (LDA) models both classes as Gaussians with shared covariance, while Quadratic Discriminant Analysis (QDA) allows class-specific covariances. Nearest Neighbor (NN) predicts labels using the class of the closest labeled training example.
Evaluation
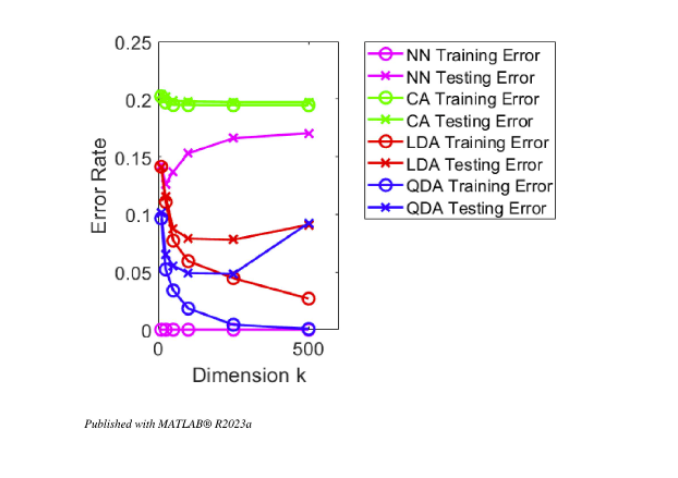
Each classifier is evaluated using training and testing error rates. Experiments are repeated across PCA dimensions \(k\) to study trade-offs between representation size, model assumptions, and accuracy.
Unsupervised Learning
The unsupervised component is Principal Component Analysis (PCA) used for dimensionality reduction. PCA identifies directions of maximum variance and projects data into a lower-dimensional subspace. The reduced representation is then fed into the supervised classifiers.
Why PCA helps
• Reduces dimensionality → faster training
• Removes noise directions
• Lets you study accuracy vs representation size
Key rule
Fit PCA on training data only, then apply the same transform to test data (no leakage).
Implementation
The implementation emphasizes consistent preprocessing and fair comparisons. Training statistics (means, covariances, PCA basis) are computed on the training set and reused for the test set. Each classifier is evaluated under the same conditions.
Pipeline
• Load + vectorize images
• Split train/test
• Optional PCA(k)
• Train classifier
• Compute error rates
What I emphasized
• Correctness + comparability
• Clear metrics (train vs test error)
• Controlled experiments (vary only k)
Results
Results were analyzed by comparing error rates across different classifiers and PCA dimensions. This revealed practical trade-offs: some models improve with higher dimensionality, while others overfit or become unstable depending on covariance assumptions and sample count.
Takeaways
• Representation matters as much as the classifier
• PCA can improve speed and sometimes generalization
• LDA/QDA behavior depends on covariance quality
What I’d add next
• Confusion matrices + ROC-style analysis
• Regularized covariance (shrinkage) for QDA
• Hyperparameter search for NN (k-NN)
Reflection
Challenges
• Feature selection affecting results
• Long training / evaluation times at high dimensions
• Environment / package friction
What I learned
• How classical classifiers behave geometrically
• PCA as a practical tool, not just theory
• How to run fair comparisons across models

 by Justin Yu
by Justin Yu